【Tensorflow2】強化学習アルゴリズムPPOを実装してみる【CartPole】

どうもこんにちは。エンジニアの竹内です。
強化学習、とりわけ方策や価値関数をニューラルネットによって近似する深層強化学習と呼ばれるものにはDQNを始めとして実に様々な手法が存在します。
今回はその中でもDQNと並んで割とポピュラーなProximal Policy Optimization(PPO)について解説しつつ、Tensorflow2を使って実際に実装していこうかと思います。
若干古いアルゴリズムですが、扱いやすく性能も良いので「これから強化学習を始めようと思うけど、手法が多すぎてなにから手をつければ良いかわからない」「そこそこ性能が良くて実装が簡単な手法を知りたい」といった方の参考になれば幸いです。

PPOとは
- ニューラルネットと目的関数
- GAE
PPOの実績
実装
結果
参考にした資料・サイト

PPOとは

まず、PPOの概要について説明していきます。
Proximal Policy Optimization(https://arxiv.org/abs/1707.06347)*1はOpenAIが2017年に公開した強化学習アルゴリズムであり、同じ方策ベースのA3C(https://arxiv.org/abs/1602.01783)やTRPO(https://arxiv.org/abs/1502.05477)等の手法と比べて高いパフォーマンスを発揮しながら実装が非常にシンプルという点で、OpenAIの標準アルゴリズムとして採用されています。

基本的な特徴は
・行動価値を推定するDQNと異なり、直接方策を改善するような勾配を求める方策勾配法という手法をとっている
・現在の方策によって得られたサンプルのみを学習に使用する方策オン型のアルゴリズムである
・離散行動と連続行動のどちらにも対応できる
といった点になります。

PPOの手法の肝は、方策勾配法によって方策を改善する際前の方策と新しい方策との比を一定の範囲にクリッピング(制限)することで、パラメータの更新に伴うな急激な方策の変化によってパフォーマンスが低下してしまうことを防ぐという点です。
PPOの元となったTRPOでは前の方策と新しい方策との間のKL-divergenceに制約を課すことで方策の急激な変化を防いでいましたが、比をクリッピングするというシンプルなアイデアでTRPOよりも高いパフォーマンスを発揮しつつ、非常にシンプルに実装が可能となりました。

以下、CartPoleの環境を例にPPOにおけるニューラルネットの構造とクリッピングが入った目的関数を見ていきたいと思います。

ニューラルネットと目的関数

PPOはA3CやTRPO等と同様に、ニューラルネットによって状態価値関数と方策関数の2つを近似するActor-Criticという手法をとっています。
価値関数と方策関数に使用するニューラルネットのパラメータは共有、非共有どちらでも実装可能ですが、今回はパラメータを共有するものとして考えます。

f:id:morika-takeuchi:20200609111802j:plain — ニューラルネットワークの構造のイメージ図（NN-SVGで作成）

このニューラルネットのパラメータ $\theta$ を更新するため、方策と状態価値に関する目的関数にエントロピー項を加えた以下の目的関数を最大化するような勾配を計算します。（実装の際にはマイナスを掛けて損失関数として計算します。）

$L^{CLIP+VF+S}_t(\theta)=L^{CLIP}_t(\theta) - c_1L^{VF}_t(\theta) + c_2L^{S}_t(\theta)$

以下、上の目的関数の中身を順番に説明していきます。

①方策

$s_t, a_t, \pi_{\theta}(a_t|s_t), V(s_t), Q(s_t, a_t)$ をそれぞれステップtにおける「状態」「行動」「方策」「状態価値」「行動価値(Q値)」として、方策の目的関数は以下で与えられます。

$L^{CLIP}_t(\theta) = \mathbb{E}_{\pi_\theta}[\min(r_t(\theta)A(s_t, a_t),\, \rm{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)A(s_t, a_t))$ ]

ただし

$r_t(\theta)=\displaystyle{\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}}$

$A(s_t, a_t) = Q(s_t, a_t) - V(s_t)$

とします。

パッと見ただけでは何をやっているのかよくわからないので一つずつ分解して考えていきましょう。
まず期待値を取っている部分に関しては、実際には現在の方策に従って得られたサンプルの平均を取ることで推定されます。
$r_t(\theta)=\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$ は前の方策と現在の方策の比です。この比が1を超えている場合、状態 $s_t$ では行動 $a_t$ を前よりも取りやすく、1を下回っている場合は前よりも取りにくくなっていると捉えることができます。
$A(s_t, a_t)$ は状態 $s_t$ で行動 $a_t$ を選択することによって得られるアドバンテージ、つまり「その行動を取ることで、状態の価値がどれぐらい改善されるか」を表した値だと考えて良いです。この値が正の場合は、よりその行動を取る確率が高くなるように、つまり $\pi_{\theta}(a|s)$ がより大きくなるようにパラメータが更新され、負の場合は逆に小さくなるように更新されます。実際には $A(s_t, a_t)$ の代わりに後で説明する $A^{GAE}(s_t, a_t)$ を使用します。
$\epsilon$ は $L$ をどれぐらいの範囲にクリッピングするかを決めるハイパーパラメータで、通常は0.1~0.3が選択されます。この値が小さければ小さいほど制約がより厳しく（方策が変化しづらく）なります。

目的関数に含まれるminやclipの役割は $A(s_t, a_t)$ の符号と $r_t$ の値で場合分けをして表とグラフにしてみるとわかりやすいです。
例えば $\epsilon=0.2$ としたときの $L^{CLIP}_t(\theta)$ は以下のように場合分けして表すことができます。

	$r_t \leq 0.8$	$0.8 \leq r_t \leq 1.2$	$1.2 \leq r_t$
$A(s_t, a_t) \geq 0$	$L=r_tA(s_t, a_t)$	$L=r_tA(s_t, a_t)$	$L=1.2A(s_t, a_t)$
$A(s_t, a_t) \leq 0$	$L=0.8A(s_t, a_t)$	$L=r_tA(s_t, a_t)$	$L=r_tA(s_t, a_t)$

f:id:morika-takeuchi:20200605105408p:plain — (Proximal Policy Optimization Algorithms, Schulman et al. 2017)

$A(s_t, a_t) \geq 0$ の場合は「より $r_t$ を大きくする」方向にパラメータが更新されますが、もう既に $r_t$ が十分大きい場合はこれ以上大きくならないように $L$ がクリッピングされます。
$A(s, a) \leq 0$ の場合は「より $r_t$ を小さくする」方向にパラメータが更新されますが、もう既に $r_t$ が十分小さい場合はこれ以上小さくならないように $L$ がクリッピングされます。
このように一回の更新によって過度に方策が変わらないように目的関数にクリッピングを行うのがPPOの手法です。

②状態価値

状態価値の目的関数は以下で与えられます。

$L^{VF}_t(\theta)= (V^\theta_t(s) - V^{targ}_t(s))^2$

$V_{targ}(s) = \displaystyle\sum_{l=0}^{\infty}\gamma^lr_{t+l}$

ただし実際の実装では $V^{targ}_t(s)$ を $A_t^{GAE} + V_t(s)$ に置き換えて計算しています。

③エントロピー項

前述の通りPPOは探索時の方策と更新する方策が同じである「オン方策型」の強化学習アルゴリズムです。
方策オン型のアルゴリズムでは、現在の方策に合わせて確率的に行動を選択することで探索を図るため、方策の確率分布が決定的になればなるほど探索は行われにくくなります。そこで、最終的な損失関数に以下のエントロピー項を追加することで、探索と搾取のトレードオフを制御します。

$L^S_t(\theta)=-\sum_{a_t}\pi(s_t, a_t)\log(\pi(s_t, a_t))$

エントロピー項は方策が決定的であるほど小さく、全ての行動を等確率で選ぶ場合が最大となります。損失にエントロピー項を加えることで早期に方策が決定的になり、探索が行われなくなってしまうことを防ぎます。

GAE

PPOでは目的関数に使用される $A(s_t, a_t)$ の推定量として、以下のGeneralized Advantage Estimator(GAE)を使用します。

$A^{GAE}(s_t, a_t)=\displaystyle\sum_{l=0}^\infty(\gamma\lambda)^l\delta_{t+l}$

$\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$

$0 \leq \lambda \leq 1$

GAEの役割をざっくりと説明すると、Advantageの推定量の分散とバイアスを調節し、学習が安定して収束するのを助けるためのものです。
$\lambda$ はGAE固有のパラメータであり0に近いほどバイアスが、1に近いほど分散が大きくなり、経験的に $\gamma$ より小さい値を取ると良いらしいということが上記のGAEの論文で触れられています。
$\lambda=1$ のとき

$A^{GAE}(s_t, a_t) = \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$

$\lambda=0$ のとき

$A^{GAE}(s_t, a_t) = \displaystyle\sum_{l=0}^\infty(\gamma)^l\delta_{t+l} = \displaystyle\sum_{l=0}^\infty(\gamma)^lr_{t+l}$

となります。
実装においてはGAEはエピソード終了までか事前に決めておいたステップ数(horizon)までの $\delta$ を使用して計算します。

PPOの実績

PPOはそのパフォーマンスの高さと実装のしやすさから、過去の強化学習のコンペティション等でも高い実績を残しています。*2
今回はそのうちのいくつかを簡単に紹介させていただきます。（コンペティションの詳細な内容などはURLから各公式webページ御覧ください。）

Unity Obstacle Tower

昨年開催されていたUnity主催のコンペです。優勝者はppoと行動模倣(Behavioral Clonig)を組み合わせた手法を使用しています。
https://blogs.unity3d.com/jp/2019/08/07/announcing-the-obstacle-tower-challenge-winners-and-open-source-release/

OpenAI Retro Contest

2018年に開催されていたOpenAIによるソニック・ザ・ヘッジホッグのステージを攻略するコンペです。joint-ppoというppoの派生手法を使用したアリババのチームが優勝しています。
https://openai.com/blog/first-retro-contest-retrospective/

Animal AI Olympics

昨年開催されていた、ケンブリッジ大学のAI研究所(Leverhulme Centre for the Future of Inteligence)とプラハのAI研究機関(GoodAI)主催のコンペです。PPOを使用したチームが優勝しています。
http://animalaiolympics.com/AAI/

1位を取った方がTwitterでアルゴリズムの概要を紹介されています。

#animalaiolympics #mlagents #ai #ReinforcementLearning
A few words about my solution:
- I used self-written ppo2 impl
- One network with two heads for value and policy
- LSTM layer in the end
- Final submission had near 70 millions of steps
- It took near 40 hours to learn
— DenysM (@DenysM88) 2019年11月12日

OpenAI Five

コンペティションではないですが、Dota2でプロチームを破ったOpenAI FiveはPPOをベースとして分散型強化学習・LSTMを組み合わせたアルゴリズムとなっています。
https://openai.com/projects/five/

Unity ML-Agents

こちらもコンペティションではないですが、Unity上で強化学習を簡単に行えるプラグインであるUnity ML-Agentsではプリセットのアルゴリズムの一つにPPOが採用されています。
https://unity3d.com/jp/machine-learning

実装

PPOの輝かしい実績をみてきたところで、ここからは実際の実装に入ります。
学習に使用する環境にはOpenAI gymのclassic controlから、CartPole-v1*3を使用します。
ブログ上のコードは説明のために簡略化して断片的に載せてあるため、全ソースコードについてはgithubを御覧ください。
使用言語はPython3, フレームワークはTensorflow2です。

メイン部分

メインのループとなる部分です。
大まかな流れは
1. 各変数の初期化
2. 1ステップごとに状態や行動、状態価値や報酬などをサンプルして保存
3. 規定のステップ数に達したらミニバッチを作成してネットワークのパラメータを更新
となります。これを延々と繰り返していきます。

def main():
    set_global_seeds(config.random_seed)  # シード値を固定
    env = gym.make(config.env_name)
    env = CartPoleWrapper(env)  # 学習がしやすいように報酬の与え方を変えるラッパーを使用
    with tf.device("/cpu:0"):  # 推論・学習を行うニューラルネットを構築
        ppo = PPO(
            num_actions=env.action_space.n,
            input_shape=env.observation_space.shape,
            config=config
        )
    num_episodes = 0
    episode_rewards = deque([0] * 100, maxlen=100)
    memory = Memory(env.observation_space.shape, config)
    reward_sum = 0
    obs = env.reset()
    # ===== 学習の開始 =====
    for t in tqdm(range(config.num_update)):
        # ===== 環境を走ってサンプルを集める =====
        for _ in range(config.num_step):
            policy, value = ppo.step(obs[np.newaxis, :])  # NNでvとpiを推論
            policy = policy.numpy()  # tensorが返ってくるのでnumpyに変換
            action = np.random.choice(2, p=policy)  # piにしたがって確率的に行動を選択
            next_obs, reward, done, _ = env.step(action)  # 行動を入力して環境を1ステップ進める
            memory.add(obs, action, reward, done, value, policy[action])  # 学習に必要な情報を保存
            obs = next_obs
            reward_sum += reward
            if done:  # エピソードが終了したらスコアを保存して環境をリセット
                episode_rewards.append(env.steps)
                num_episodes += 1
                reward_sum = 0
                obs = env.reset()
        _, last_value = ppo.step(obs[np.newaxis, :])
        memory.add(None, None, None, None, last_value, None)  # deltaの計算用にvalueだけ1ステップ分余計に保存する

        memory.compute_gae()  # GAEを計算
        # ===== ニューラルネットのパラメータを更新 =====
        for _ in range(config.num_epoch):
            idxes = [idx for idx in range(config.num_step)]  # サンプルするためのインデックスを用意
            random.shuffle(idxes)
            for start in range(0, len(memory), config.batch_size):  # シャッフルしたインデックスからミニバッチサイズ分の区間を取っていく
                minibatch_indexes = idxes[start:start+config.batch_size]
                batch_obs, batch_act, batch_adv, batch_sum, batch_pi_old = memory.sample(minibatch_indexes)  # ミニバッチを作成
                loss, policy_loss, value_loss, entropy_loss, policy, kl, frac = ppo.train(batch_obs, batch_act, batch_pi_old, batch_adv, batch_sum)  # モニタリング・デバッグ用に各種ロスを受け取っておく
        memory.reset()  # 次の探索のためにメモリーをリセット

メモリー

探索によって集めたサンプルは学習用にメモリクラスに保存しておきます。
DQNでいうリプレイバッファに当たる部分ですが、PPOではパラメータ更新ごとに収集したサンプルを破棄します。
また、後に必要となるGAEを計算するために1ステップごとに $\delta_t = r_t + \gamma V_{t+1} - V_t$ の値を計算しておきます。
この際、1ステップ先の状態価値を使用する必要があるため、1ステップ分遅延させて計算します。
つまり、最初のステップでは何も計算せず、ステップ1で $\delta_0$ を計算、ステップ2で $\delta_1$ を計算…ステップtで $\delta_{t-1}$ というように計算していきます。そのためvalueを保存する配列のサイズは1つ分余計に取ってあります。
ステップtでエピソードが終了していた場合、 $V_{t+1}$ は0となることに注意します。

class Memory:
    def __init__(self, obs_shape, hparams):
        self._hparams = hparams
        self.size = self._hparams.num_step
        self.obses   = np.zeros((self.size, )+obs_shape)
        self.actions = np.zeros((self.size, ))
        self.rewards = np.zeros((self.size,   1))
        self.dones   = np.zeros((self.size,   1))
        self.values  = np.zeros((self.size+1, 1))  # valueだけサイズを1つ大きく取る
        self.policy  = np.zeros((self.size,   1))
        self.deltas  = np.zeros((self.size,   1))
        self.discounted_rew_sum = np.zeros((self.size, 1))
        self.gae = np.zeros((self.size, 1))
        self.sample_i = 0  # サンプルをメモリに保存するためのポインタ

    def add(self, obs, action, reward, done, value, policy):
        if self.sample_i < len(self.obses):
            self.obses[self.sample_i] = obs
            self.actions[self.sample_i] = action
            self.rewards[self.sample_i] = reward
            self.dones[self.sample_i] = done
            self.values[self.sample_i] = value
            self.policy[self.sample_i] = policy

        if self.sample_i > 0:  # 最初のサンプルではdeltaを計算しない
            self.deltas[self.sample_i - 1] = self.rewards[self.sample_i - 1] + self._hparams.gamma * value * (1 - self.dones[self.sample_i - 1]) - self.values[self.sample_i - 1]
        self.sample_i += 1

GAEの計算

事前に計算しておいた $\delta$ を用いてGeneralized Advantage Estimatorを後ろからさかのぼって計算します。
最後の状態のGAEは $\delta$ と等しく、それ以前は次の状態のGAEを $\gamma * \lambda$ で割り引いた値に $\delta$ の値を足したものになります。ただしエピソードをまたいで計算しないようにエピソードの終了フラグがTrueの場合はそれまでに計算したGAEの値を0に戻します。
今回の実装ではGAEを計算するまでに128ステップ分の経験を保存しているため、途中でエピソードが終了していなければ最大128ステップ先の $\delta$ まで使用されることになります。
$A^{GAE}(s_t, a_t)=\displaystyle\sum_{l=0}^{\min(end_t, 128)}(\gamma\lambda)^l\delta_{t+l}$

    def compute_gae(self):

        self.gae[-1] = self.deltas[-1]
        for t in reversed(range(self.size-1)):
            self.gae[t] = self.deltas[t] + (1 - self.dones[t]) * (self._hparams.gamma * self._hparams.lambda_) * self.gae[t + 1]
        self.discounted_rew_sum = self.gae + self.values[:-1]
        self.gae = (self.gae - np.mean(self.gae)) / (np.std(self.gae) + EPS)

損失の計算

パラメータを更新するための損失を定義に従って実装します。オプティマイザはAdamを使用します。logの中身や分数の分母が0にならないようにする点や損失関数の符号などに注意します。
GradientTapeはコンテクスト内で行う計算を監視して自動微分を行う、Eager Excution特有の仕組みです。(公式ドキュメント)
コンテクスト内の計算は基本的にtensorを使用して行うようにします（numpyなどを挟むと勾配がnoneで返ってくるので注意が必要です。）
@tf.functionデコレータはつけたほうが高速になる場合が多いですが、デバッグの際にはコメントアウトしたほうが良いです。

class PPO(tf.Module):
    def __init__(self, num_actions, input_shape, config):
        super(PPO, self).__init__(name='ppo_model')
        self.num_actions = num_actions
        self.input_shape = input_shape
        self.batch_size = config.batch_size
        self.config = config

        self.policy_value_network = self._build_model()
        self.optimizer = tf.keras.optimizers.Adam(learning_rate=config.learning_rate)
        self.gradient_clip = config.gradient_clip

    @tf.function
    def train(self, obs, action, pi_old, advantage, rew_sum):
        # GradientTapeコンテクスト内で行われる計算は勾配を記録することが出来ます。
        with tf.GradientTape() as tape:
            policy, value = self.policy_value_network(obs)
            value = tf.squeeze(value)
            one_hot_action = tf.one_hot(action, self.num_actions)
            pi = tf.squeeze(tf.reduce_sum(policy * one_hot_action, axis=1, keepdims=True))
            ratio = tf.divide(pi, pi_old + EPS)  # log内や割り算で0が発生し、パラメータがnanになるのを避けるため予め小さい数を加えます
            clipped_advantage = tf.where(advantage > 0, (1+self.config.clip)*advantage, (1-self.config.clip)*advantage)
            l_clip = (-1) * tf.reduce_mean(tf.minimum(ratio * advantage, clipped_advantage))  # 損失を定義する必要があるので最大化したいものにはマイナスを付けます
            l_vf = tf.reduce_mean(tf.square(rew_sum-value))
            entropy = - tf.reduce_sum(policy * tf.math.log(policy + EPS), axis=1)
            l_ent = tf.reduce_mean(entropy)
            loss = l_clip + l_vf * self.config.vf_coef - l_ent * self.config.ent_coef  # エントロピーは最大化するように符号を付けます
        grads = tape.gradient(loss, self.policy_value_network.trainable_variables)  # 記録した計算のパラメータに関する勾配を取得します
        if self.gradient_clip is not None:  # 勾配を一定の範囲にクリッピングします
            clipped_grads = []
            for grad in grads:
                clipped_grads.append(tf.clip_by_norm(grad, self.gradient_clip))
            grads = clipped_grads
        grads_and_vars = zip(grads, self.policy_value_network.trainable_variables)
        self.optimizer.apply_gradients(grads_and_vars)  # optimizerを適用してパラメータを更新します
        # ↓ここから先はデバッグなどのために監視する値なので学習には不要です
        new_policy, _ = self.policy_value_network(tf.convert_to_tensor(obs, dtype=tf.float32))
        new_prob = tf.reduce_sum(new_policy * one_hot_action, axis=1)
        kl = tf.reduce_mean(pi * tf.math.log(new_prob+EPS) - pi * tf.math.log(pi+EPS))
        clipfrac = tf.reduce_mean(tf.cast(tf.greater(tf.abs(ratio - 1.0), self.config.clip), tf.float32))

        return loss, l_clip, l_vf, l_ent, policy, kl, clipfrac

各種パラメータ

ハイパーパラメータの値はStable Baselinesのものを参考にさせていただきました。

class Config(NamedTuple):
    # learning config
    env_name: str = "CartPole-v1"  # OpenAI gymの環境名
    seed: int = 1234  # tensorflow numpy randomのシード値
    num_update: int = 3000  # 学習時の総イテレーション数
    log_step: int = 100  # ログを表示する頻度
    play: bool = False  # 学習終了時に描画して再生
    # hyper-parameters
    batch_size: int = 32  # バッチサイズ
    num_epoch: int = 4  # エポック数
    num_step: int = 128  # 1イテレーションで保存するサンプルの総数(horizon)
    num_unit: int = 64  # fc層のunit数
    gamma: float = 0.99  # 割引率
    lambda_: float = 0.95  # GAEの割引率
    clip: float = 0.2  # クリップする範囲
    vf_coef: float = 0.5  # 価値損失の係数
    ent_coef: float = 0.01  # エントロピー項の係数
    learning_rate: float = 2.5e-4  # 学習率
    gradient_clip: float = 0.5  # 勾配をクリップする範囲

結果

上記の実装でCartPole-v1を学習させてみた結果です。(スペックはIntel i7 6core RAM64GB, cpuのみを使用)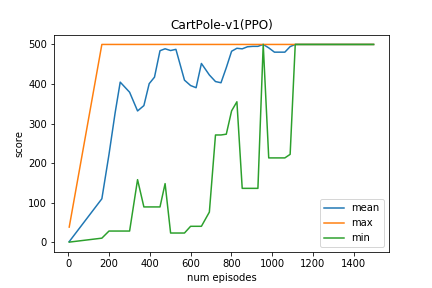

f:id:morika-takeuchi:20200615124918p:plain — 学習時のスコアの推移

およそ10分~15分、2500エピソード程度の学習で最高スコアの500をコンスタントに記録するようになります。
今回は実装を簡潔にするため学習環境の並列化は行っていませんが、複数のエージェントを並列してサンプリングすることでさらなる高速化が望めます。

参考にした資料・サイト

・Proximal Policy Optimization Algorithms(arXiv)
https://arxiv.org/abs/1707.06347
・Proximal Policy Optimization(OpenAI blog)
https://openai.com/blog/openai-baselines-ppo/
・Proximal Policy Optimization(OpenAI Spinning Up)
https://spinningup.openai.com/en/latest/algorithms/ppo.html
・OpenAI Baselines
https://github.com/openai/baselines/tree/tf2
・High-Dimensional Continuous Control Using Generalized Advantage Estimation(arXiv)
https://arxiv.org/abs/1506.02438
・Stable Baselines
https://stable-baselines.readthedocs.io/en/master/modules/ppo2.html
・NN-SVG
https://alexlenail.me/NN-SVG/

*1:PPOにはクリッピングを行うPPO-ClipとKL-divergense項を加えるPPO-Penaltyの二種類がありますが、本記事では前者の方を指すことにします。

*2:強化学習のコンペ自体がだいぶマイナーですが…

*3:v0だと最大ステップ数200、v1だと500になります。

Morikatron Engineer Blog

モリカトロン開発者ブログ