はじめに
こんにちは。モリカトロンでエンジニアをやっている竹内です。
この記事は【DQfD】人間のプレイを参考にして学習する強化学習アルゴリズムを実装してみる【前半】 - Morikatron Engineer Blogの後半となります。前半の記事をまだご覧になっていない方は、そちらの方を先にお読みいただくことをおすすめします。
前半では人間のプレイを参考にしつつ強化学習を行うDeep Q-Learning from Demonstrations(https://arxiv.org/abs/1704.03732)というアルゴリズムを紹介させていただきました。今回は実際にDQfDを実装しながら、Atari2600の中で最も学習が難しいとされているMontezum's Revengeというゲームを学習していきたいと思います。
今回学習に使用したコードはgithubにて公開しています。(Python3+Tensorflow2.0)
Montezuma's Revengeについて
実装に入る前に今回学習するMontezuma's Revenge(以下Montezuma)というゲームについて少し触れておきます。
このゲームは骸骨や蛇などの敵をよけながら鍵や松明などのアイテムを集めてダンジョンを攻略していき、最深部まで到達すればステージクリアとなる、いわゆる横スクロールアクションゲームです。
Montezumaがどのようなゲームなのかについては実際のプレイ動画を見ていただくとイメージし易いかと思います。
Montezumas Revenge 242900pts for 2600 NEW HSC S5 Week 30
特徴的なのはプレイヤーがコントロールするキャラクターが極端に弱く、少しでも高いところから落下したり、敵に触れたりすると残機が減り部屋の最初からやり直しとなってしまう点です。それゆえに操作するタイミングも非常にシビアとなっています。
強化学習という観点でいえばこのゲームはAtari2600の中でもPitfallと並んで群を抜いて学習が難しいタイトルの一つとされており、その難しさゆえにいくつかの論文では強化学習アルゴリズムにおけるベンチマークの一つとしてしばしば取り上げられています。*1
このゲームにおいて学習を困難にさせている要因としては主に以下の2点が挙げられます。
- 報酬が疎で探索が難しい
- 時間差で作動するギミックとアルゴリズムとの相性が悪い
1に関しては論文でもよく指摘される側面であり、以下のOpenAIのブログにおいても詳細に述べられています。
openai.com
より具体的に表現すると「報酬を手に入れるまでに一連の限られた動作を正確に行う必要がある」と言い換えることができます。
多くの強化学習アルゴリズムでは完全にランダムな行動を初期方策として、偶然得られた報酬をもとにより良い方策を学習していきます。例えばブロック崩しであれば「ランダムに行動していたら偶然バーに弾が当たって報酬を得られれた」という経験の積み重ねで徐々に「バーを弾に当てる」という方策を学習していきます。
ところがMontezumaの場合、最初の報酬である鍵を手に入れるまでに「連続した下移動で最初のはしごを降りる」「連続した右移動の後、限られたタイミングでジャンプし棒に掴まる」といった一連の決められた行動を行う必要があり、しかも一歩間違えれば即ライフを失い再びスタートからやり直すことになります。
鍵を手に入れるために要する行動数が大体80~100ステップ分であり*2、1フレームにつき4種類の行動選択肢があると考えても*3完全にランダムで行動していては、たとえ1億ステップ探索を行っていても最初の報酬にすらありつくことは絶望的です。
DQfDでは初期方策をランダムな方策とするのではなく、デモデータから事前学習した方策とすることで探索が難しい環境でも効率的な学習を可能とします。
2に関してはあまり言及されることが少ないのですが、重要な側面だと考えています。
多くの強化学習アルゴリズムは、学習を行う環境がマルコフ決定過程(MDP)であること、つまり「ある行動をした後の状態は、現在の状態と行動のみによって確率的に決定される」ことを前提としています。DQNをはじめとしたいくつかの強化学習アルゴリズムではAtariのゲームを学習する際、NNに入力する状態を直近4フレームを重ねたものとしています。これによって例えばBreakout(ブロック崩し)であれば、現在の弾の位置だけでなく次に弾がどの位置に来るか(ボールの速度)についても直近4つの画面から理論上判別することができるため、MDPの前提を満たすことが出来ます。
ところがMontezumaを含むいくつかのatariのゲームでは、直近4フレームのスタックではMDPの前提を明らかに満たさない状況が存在します。*4
例えばある部屋には触れると即ライフを失うビームが時間差で出現するギミックがありますが、直近4フレームを見るだけでは次のフレームでビームが出現するか否かについては判別することが出来ません。
また、ある部屋には時間差で足場が消えるギミックがありますが、こちらも直近4フレームを見るだけでは次のフレームで足場が存在するか否かについて判別することは不可能です。

ギミック以外についても、ステージの中に完全に同じデザインの部屋がいくつか存在する、或いは同じ部屋を攻略のために往復する必要があるなどMDPの前提を満たさないと考えられる状況が存在します。*5
したがってMontezumaのような4フレームを優に超える時間差ギミックが存在する場合、直近4フレームをスタックする手法ではMDPの前提を満たさず、理論上は最適な方策を求めることが困難になると考えられます。
DQfDにおいてもスタックするフレーム数は4フレームであり、特にRNNの構造なども用いられていないため時間差ギミックを完全に攻略することは難しいものの、デモデータの存在によりある程度安定して攻略することが可能です。
DQfD playing Montezuma's Revenge
元論文の著者実装によるDQfDがMontezumaを攻略する動画ですが、時間差で足場が消える部屋で苦戦している印象を受けます。また、1:08付近では足場が途中で消滅する可能性を考慮していないような挙動をしています。
実装
前置きが長くなりましたが、いよいよ実装に移りたいと思います。
元論文に記載されている疑似コードを見ると、大枠はDQNとあまり変わらないことがわかります。DQNの実装をベースとしてデモを用いた模倣学習部分を追加していけば良さそうです。

(T. Hester et al., 2017 "Deep Q-learning from Demonstrations")
そこで、まずはじめにPrioritized Dueling Double DQN(以下単にDQNと書きます)を実装していく必要があります。もちろん0からこれらを実装しても良いのですが、DQNの実装自体はだいぶ手垢がついてきていますし、主目的ではない部分にかける手間も極力減らしたいので、今回はOpenAIが公開している強化学習アルゴリズムの実装セットであるOpenAI BaselinesのDQNの実装をベースとして使用させていただきます。OpenAI BaselinesではDQN、PPO、A2Cなど主要な強化学習アルゴリズムがTensorflowで実装されています。学習環境の並列化や学習用のラッパーなども揃っており、コードも読みやすいので実装を見るだけでも非常に良い勉強になります。また、今回のように新しいアルゴリズムを実装する際の足掛かりにもなります。(パフォーマンスの比較にも使えます)
OpenAI Baselinesのセットアップについてはhttps://github.com/openai/baselinesをご覧ください。
また、ブログ上のコードは説明のために簡略化した疑似コードとなっております。
全ソースコードについてはgithubを御覧ください。
OpenAI Baselinesのdeepqの実装に倣ってディレクトリ構造はこんな感じになっています。
DQfD
├ common/ (Atariのラッパーやらセグ木やら色々便利なものをまとめておく)
├ __init__.py
├ dqfd.py (学習のループを回す)
├ dqfd_learner.py (行動の選択やパラメータの更新などを記述する)
├ make_demo.py (ゲームをプレイしてデモを作成する)
├ models.py (NNの構造を記述する)
├ replay_buffer.py (リプレイバッファ)
└ run_atari.py (メイン関数)
学習の大枠
学習の主な部分はdqfd.pyのlearn関数内で行います。
ループは事前学習部分と探索部分で2つ存在しますが、パラメータの更新部分はどちらもほとんど同じです。
# dqfd.py def learn(): # ===== 事前学習部分 ===== for t in range(pre_train_timesteps): # リプレイバッファからミニバッチを作成 experience = replay_buffer.sample(batch_size, beta=prioritized_replay_beta0) batch_idxes = experience[-1] # 優先度更新用 obses_t, actions, rewards, obses_tp1, dones, is_demos, obses_tpn, rewards_n, dones_n, weights = tuple(map(tf.constant, experience[:-1])) # ミニバッチをモデルに送りパラメータを更新 td_errors, n_td_errors, loss_dq, loss_n, loss_E, loss_l2, weighted_error = model.train(obses_t, actions, rewards, obses_tp1, dones, is_demos, weights, obses_tpn, rewards_n, dones_n) # 優先度を更新 new_priorities = np.abs(td_errors) + np.abs(n_td_errors) + demo_prioritized_replay_eps replay_buffer.update_priorities(batch_idxes, new_priorities) # 1万ステップごとにターゲットネットワークを更新 if t > 0 and t % target_network_update_freq == 0: model.update_target() # ===== 探索部分 ===== obs = env.reset() # 環境をリセット for t in range(total_timesteps): # 状態をモデルに送り、ε-greedy法で行動を選択 action, epsilon, _, _ = model.step(tf.constant(obs), update_eps=update_eps, **kwargs) new_obs, rew, done, _ = env.step(action) # テンポラリバッファに追加 temp_buffer.append((obs, action, rew, new_obs, done, is_demo)) # 10サンプル集まったら報酬和を計算してリプレイバッファに追加 if len(temp_buffer) == n_step: n_step_sample = get_n_step_sample(temp_buffer, gamma) replay_buffer.add(*n_step_sample) obs = new_obs # 4ステップごとにパラメータを更新 if t % train_freq == 0: experience = replay_buffer.sample(batch_size, beta=beta_schedule.value(t)) batch_idxes = experience[-1] obses_t, actions, rewards, obses_tp1, dones, is_demos, obses_tpn, rewards_n, dones_n, weights = tuple(map(tf.constant, experience[:-1])) td_errors, n_td_errors, loss_dq, loss_n, loss_E, loss_l2, weighted_error = model.train(obses_t, actions, rewards, obses_tp1, dones, is_demos, weights, obses_tpn, rewards_n, dones_n) new_priorities = np.abs(td_errors) + np.abs(n_td_errors) + demo_prioritized_replay_eps * is_demos + prioritized_replay_eps * (1. - is_demos) replay_buffer.update_priorities(batch_idxes, new_priorities) # 1万ステップごとにターゲットネットワークを更新 if t % target_network_update_freq == 0: model.update_target()
10ステップ分の状態遷移を保存
10ステップTD誤差を計算するため、リプレイバッファに現在の状態とセットで10ステップ先の状態や割引報酬和を保存する必要があります。そのため、キューに直近10ステップ分の状態遷移を一時的に保存し、10ステップたまった時点で累積割引報酬和を計算してからリプレイバッファに保存していきます。
# dqfd.py def get_n_step_sample(buffer, gamma): reward_n = 0 # 累積割引報酬和を計算 for i, step in enumerate(buffer): reward_n += step[2] * (gamma ** i) obs = buffer[0][0] action = buffer[0][1] rew = buffer[0][2] new_obs = buffer[0][3] done = buffer[0][4] is_demo = buffer[0][5] n_step_obs = buffer[-1][3] done_n = buffer[-1][4] return obs[0], action, rew, new_obs[0], float(done), float(is_demo), n_step_obs[0], reward_n, done_n
累積割引報酬和を計算する際、前ステップの計算結果を利用して再帰的に計算する方が速そうなのですが、floatの精度の影響で色々上手く行かなかったので今回は愚直に計算しています。
リプレイバッファの改造
DQNにおけるリプレイバッファの機能は、ゲーム内を探索することによって得られた状態遷移や行動などのサンプルデータを後の学習のために溜め込んでおくものです。これによってデータ同士の相関を減らし、学習を安定化させます。
今回の実装においては探索によって得られるデータと予め作成したデモデータを同じリプレイバッファに保存します。通常、リプレイバッファが溢れた際は古いデータから削除されていきますが、デモデータは学習を通して削除せず残しておく必要があることに注意します。また、リプレイバッファには現在の状態と1ステップ先の状態遷移に加えて10ステップ先の状態遷移を加える必要があります。
リプレイバッファはreplay_buffer.pyに以下のように実装しています。
# replay_buffer.py class ReplayBuffer(object): def __init__(self, size): self._storage = [] self._maxsize = size self._next_idx = 0 self.demo_len = 0 def add(self, obs_t, action, reward, obs_tp1, done, is_demo, obs_tpn=None, reward_n=None, done_n=None): data = (obs_t, action, reward, obs_tp1, done, is_demo, obs_tpn, reward_n, done_n) # 溢れるまでデータを追加 if self._next_idx >= len(self._storage): self._storage.append(data) # データ内のis_demoフラグを確認 elif self._storage[self._next_idx][5]: # 上書きしないようにindexをスキップ self._next_idx = self.demo_len self._storage[self._next_idx] = data else: self._storage[self._next_idx] = data self._next_idx = (self._next_idx + 1) % self._maxsize # ==一部省略==
学習にはこのリプレイバッファクラスを継承した優先度付きリプレイバッファを使用します。*6
優先度付きリプレイバッファの実装はDQNのものをそのまま使用することが出来ます。
Atariラッパーの追加
画面のリサイズやグレースケール化、フレームのスキップ、4画面分のスタックなどの前処理はgymのラッパーによって行います。今回はDQNに使用されているラッパーのほかに報酬のlogスケール化、残機表示のマスク*7のラッパーを新しく追加します。
追加するAtariラッパーはcommon/atari_wrappers.pyに以下のように実装しています。
# ==一部省略== class LogRewardEnv(gym.RewardWrapper): def __init__(self, env): gym.RewardWrapper.__init__(self, env) def reward(self, reward): # 報酬をlogスケールに変換 return np.sign(reward) * np.log(1.0 + abs(reward)) class MaskLives(gym.ObservationWrapper): # Montezumのみ def __init__(self, env): super().__init__(env) def observation(self, obs): # 残機表示部分のピクセル値を0にする obs[14:21, :, :] = 0 return obs # ==一部省略== # Atariラッパー def make_atari(env_id, max_episode_steps=None): # 環境の作成 env = gym.make(env_id) assert 'NoFrameskip' in env.spec.id # エピソードリセット後、数フレーム何もしないことで過学習を防ぐ env = NoopResetEnv(env, noop_max=30) # 2フレームずつピクセルの最大値を取る&4フレームスキップ env = MaxAndSkipEnv(env, skip=4) # エピソードの時間制限 if max_episode_steps is not None: env = TimeLimit(env, max_episode_steps=max_episode_steps) return env # Baselinesで実装されているdeepmindスタイルのAtariラッパーに上記を追加 def wrap_deepmind(env, episode_life=False, clip_rewards=False, frame_stack=False, scale=False, log_rewards=True): # 残機が減少したらエピソードの終わりとする→False if episode_life: env = EpisodicLifeEnv(env) # エピソード開始時にFIREアクションをとる→True if 'FIRE' in env.unwrapped.get_action_meanings(): env = FireResetEnv(env) # 残機を非表示 env = MaskLives(env) # リサイズ&グレースケール化 env = WarpFrame(env) # ピクセル値を標準化→True if scale: env = ScaledFloatFrame(env) # 報酬を-1, 0, 1にクリップ→False if clip_rewards: env = ClipRewardEnv(env) # 報酬をlogスケール化→True if log_rewards: env = LogRewardEnv(env) # 4フレーム分をスタック→True if frame_stack: env = FrameStack(env, 4) return env
デモの作成
デモデータの作成には実際にゲームをプレイする必要があります。
OpenAI gymにpygameを利用したテストプレイ用の実装(gym/play.py at master · openai/gym · GitHub)があるため、これをデモデータの作成用に少し改造します。*8
デモは
trajectory = [エピソード1, エピソード2, …]
エピソードN = [(画面, 行動, 報酬, 次の画面, 終了フラグ), …]
という形でpickleを使って保存します。
# make_demo.py def play(env, transpose=True, fps=30, zoom=None, callback=None, keys_to_action=None): # ==一部省略== env.reset() running = True env_done = True save_trajectory = True # デモを保存するフラグ trajectories = [] # デモをエピソードごとに保存するリスト episode_trajectory = [] # 1つのエピソードを保存するリスト while running: if env_done: env_done = False obs = env.reset() if len(episode_trajectory) > 0 and save_trajectory: # エピソードを追加 trajectories.append(episode_trajectory) episode_trajectory = [] save_trajectory = True else: action = keys_to_action.get(tuple(sorted(pressed_keys)), 0) prev_obs = obs obs, rew, env_done, info = env.step(action) # 状態遷移を保存 episode_trajectory.append((np.array(prev_obs), np.array(action, dtype='int64'), rew, np.array(obs), env_done)) # pygameのイベント処理 for event in pygame.event.get(): # test events, set key states if event.type == pygame.KEYDOWN: if event.key in relevant_keys: pressed_keys.append(event.key) # Backspaceでデモを保存せずにエピソードをリセット elif event.key == pygame.K_BACKSPACE: save_trajectory = False env_done = True # Enterでデモを保存しつつエピソードをリセット elif event.key == pygame.K_RETURN: save_trajectory = True env_done = True # プレイ終了 elif event.key == pygame.K_ESCAPE: running = False elif event.type == pygame.KEYUP: if event.key in relevant_keys: pressed_keys.remove(event.key) elif event.type == pygame.QUIT: running = False pygame.display.flip() clock.tick(fps) pygame.quit() return trajectories def main(): # ==一部省略== env = make_env(args.env, args.seed, wrapper_kwargs={'frame_stack': True}) trajectories = play(env, zoom=4, fps=20) print("num episodes", len(trajectories)) os.makedirs(dir_path, exist_ok=True) with open(os.path.join(dir_path, taskName), mode="wb") as f: pickle.dump(trajectories, f)
損失関数の導入
dqfd_learner.pyのtrain関数に、DQN用に既に実装されている1ステップTD誤差に加えて10ステップTD誤差、Large Mergin Classification Loss*9、L2正則化誤差も同様に実装していきます。
# dqfd_learner.py class DQfD(tf.Module): # ==一部省略== @tf.function() def train(self, obs0, actions, rewards, obs1, dones, is_demos, importance_weights, obsn=None, rewards_n=None, dones_n=None): # コンテクスト内の計算について勾配を計算する with tf.GradientTape() as tape: # ====================1-step loss=================== # Double DQNを使用 # Policyネットワークによる現在の状態に対する全行動のQ値 q_t = self.q_network(obs0) one_hot_actions = tf.one_hot(actions, self.num_actions, dtype=tf.float32) # 実際に選択されたQ値 q_t_selected = tf.reduce_sum(q_t * one_hot_actions, 1) # Targetネットワークによる次の状態に対する全行動のQ値…(1) q_tp1 = self.target_q_network(obs1) # Policyネットワークによる次の状態に対する全行動のQ値…(2) q_tp1_using_online_net = self.q_network(obs1) # (2)のQ値を最大化する行動…(3) q_tp1_best_using_online_net = tf.argmax(q_tp1_using_online_net, 1) # (1)において(3)を選択したときのQ値 q_tp1_best = tf.reduce_sum(q_tp1 * tf.one_hot(q_tp1_best_using_online_net, self.num_actions, dtype=tf.float32), 1) dones = tf.cast(dones, q_tp1_best.dtype) # エピソードが終了していたらQ値をマスクする q_tp1_best_masked = (1.0 - dones) * q_tp1_best # ターゲットとなる割引報酬の推定値 q_t_selected_target = rewards + self.gamma * q_tp1_best_masked # ターゲットについては勾配を計算しない td_error = q_t_selected - tf.stop_gradient(q_t_selected_target) # Huber Lossを使用 loss_dq = huber_loss(td_error) # ====================n-step loss=================== q_tpn = self.target_q_network(obsn) # 1ステップTD誤差と同様にDouble DQNを使用 q_tpn_using_online_net = self.q_network(obsn) q_tpn_best_using_online_net = tf.argmax(q_tpn_using_online_net, 1) q_tpn_best = tf.reduce_sum(q_tpn * tf.one_hot(q_tpn_best_using_online_net, self.num_actions, dtype=tf.float32), 1) dones_n = tf.cast(dones_n, q_tpn_best.dtype) q_tpn_best_masked = (1.0 - dones_n) * q_tpn_best q_tn_selected_target = rewards_n + (self.gamma ** self.n_step) * q_tpn_best_masked n_td_error = q_t_selected - tf.stop_gradient(q_tn_selected_target) loss_n = self.lambda1 * huber_loss(n_td_error) # ==========large margin classification loss========= # サンプルがデモ由来かどうか判別するフラグ is_demo = tf.cast(is_demos, q_tp1_best.dtype) margin_l = self.exp_margin * (tf.ones_like(one_hot_actions, dtype=tf.float32) - one_hot_actions) margin_masked = tf.reduce_max(q_t + margin_l, 1) loss_E = self.lambda2 * is_demo * (margin_masked - q_t_selected) # ==========L2 loss========= loss_l2 = self.lambda3 * tf.reduce_sum([tf.reduce_sum(tf.square(variables)) for variables in self.q_network.trainable_variables]) # すべての損失の重み付き和を取る all_loss = loss_n + loss_dq + loss_E # 重点サンプリングによる重み付き和を取る weighted_error = tf.reduce_mean(importance_weights * all_loss) + loss_l2 grads = tape.gradient(weighted_error, self.q_network.trainable_variables) # 勾配を一定範囲にクリッピング if self.grad_norm_clipping: clipped_grads = [] for grad in grads: clipped_grads.append(tf.clip_by_norm(grad, self.grad_norm_clipping)) grads = clipped_grads grads_and_vars = zip(grads, self.q_network.trainable_variables) # Adam Optimizerでパラメータを更新 self.optimizer.apply_gradients(grads_and_vars) return td_error, n_td_error, loss_dq, loss_n, loss_E, loss_l2, weighted_error
実験
実際にデモデータを作成し、実装したコードを使用して学習を回していきます。デモデータには30000スコアを取得し、かつステージ1をクリアしたデモ5エピソードを使用しました。*10
学習にはTitan RTXを使用し、0.75Mステップの事前学習+2.4Mステップの探索と学習に約87時間を要しました。
使用したデモはこんな感じです。

結果
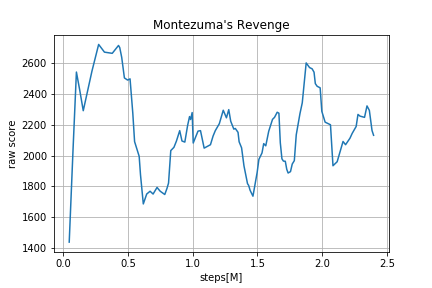
直近100エピソードの平均スコアを10エピソードごとにプロットした図です。元の論文で検証されている200Mステップまでは検証できていませんが、事前学習を終えてからかなり早い段階で高いスコアを出すことができています。また、いくつかのエピソードでは10000を超えるスコアを記録することが確認できました。
最も高いスコアを記録したチェックポイントによるプレイを動画にしてみました。
【DQfD】AI playing Montezuma's Revenge Atari2600【score12100】
デモには及びませんが正しいルートで12100点を獲得。クリア手前まで攻略できています。素晴らしい。
まとめ
人間のプレイを参考にして学習を行う強化学習アルゴリズムDQfDを紹介、実装しました。DQfDには派生手法であるApe-X DQfD([1805.11593] Observe and Look Further: Achieving Consistent Performance on Atari)とR2D3([1909.01387] Making Efficient Use of Demonstrations to Solve Hard Exploration Problems)が存在するため、そちらについても今後実装して記事にできたらと思っています。
また、今回実装したコードに関して不明な点や改善点やバグ、追加検証などございましたら、是非ブログのコメントやgithubのissues等に挙げていただけるとありがたいです。
References
- T. Hester et al., 2017, Deep Q-learning from Demonstrations
https://arxiv.org/abs/1704.03732
- T. Pohlen et al., 2018 Observe and Look Further: Achieving Consistent Performance on Atari
https://arxiv.org/abs/1805.11593
- Open AI Learning Montezuma’s Revenge from a Single Demonstration(BLOG)
https://openai.com/blog/learning-montezumas-revenge-from-a-single-demonstration/
- OpenAI Baselines
*1:[1606.01868] Unifying Count-Based Exploration and Intrinsic Motivation[1810.12894] Exploration by Random Network Distillation [1901.10995] Go-Explore: a New Approach for Hard-Exploration Problems など
*2:4フレームのスキップを入れた場合で換算しています
*3:実際は18の選択肢がありますが、多く場合において同様な行動(RIGHTとDOWN RIGHTなど)が存在するためこのように概算しています
*4:[1507.06527] Deep Recurrent Q-Learning for Partially Observable MDPsの論文でも似たような指摘があります
*5:実際には取得スコアの表示をもとに判別することができているようですが、スコアのスケールに依存しますし、何かのきっかけで攻略順が変化すると挙動が乱れる可能性があります。
*6:優先度付きリプレイバッファでは各データがサンプルされる優先度=重みをセグメント木というデータ構造を利用して保存しています。何十万というサンプルから重み付きサンプリングによってミニバッチを作成する際、セグメント木を利用することで計算量を抑えることが出来ます。また、サンプルの抽出を行う際はバッチサイズに応じた層化抽出を行っています。詳しく[1511.05952] Prioritized Experience Replayの論文を参照
*7:Ape-X DQfDの論文[1805.11593] Observe and Look Further: Achieving Consistent Performance on Atariに記載がある手法です。デモではほとんど残機を減らしていないということもあり、残機をマスクしないと探索中に減った場合にその後の方策が著しく乱れる傾向にあります。(スコアが1400で頭打ちになりました。)ただしこれについてはノイズである残機表示に過剰に適合していると言わざるを得なく、個人的には少々姑息な手法かなと思っています…
*8:学習時とデモ作成時の環境を揃えるために、フレームスキップなどのラッパーを通しているため、かなりプレイしにくいです… ラッパーを通さない環境で作ったデモを後から加工する方が良いかもしれません。
*9:丁度よい訳語がなさそうなのでそのまま表記します
*10:Montezumaの鬼難易度故に、5回クリアするのに2時間ぐらいかかりました…