「なぜトイレットペーパーはなくなるのか」
なぜ、こうした禍(COVID-19)があると、トイレットペーパーがなくなってしまうのか?
オイルショックの時の経験は、なんで活かされないのか?
こたえはこうだ。
「人間だもの」
今回はそのことについての簡単なお話。
「ゲーム理論」と呼ばれる学問がある。
ビデオゲームがいいの、悪いのなどについての理論ではなく、「ゲーム」という言葉の本来の意味である「あるルールの上で行われる競争や活動」についての学問である。
私たちが集団でいるとき、どういう考えに行き着きやすいか、どーしてそう考えてしまうのかと言ったことを数学的なモデルを用いて研究する学問のことである。
きっと、何が何やらだと思うw
ふだんの社会生活では、お互いの損得が複雑に絡み合っている。こちらが得をすれば他が損をする。お互い得することも、お互い損することもある。
他もまた自分が得するように動くはずだから、それを予測しながら、あるときは協調して、あるときは反目して対応しよう。
そうした心理作用が働くというか、戦略を考える。
一見すると複雑すぎて予測のしようがない動向のように感じるが、意外とシンプルなモデルでうまく説明できるのだ。
ざっとそういう学問である。
発案者は、フォン・ノイマンとオスカー・モルゲンシュテルン。ノイマンは、今のコンピュータ(ノイマン型コンピュータ)の仕組みを考えた、古今東西の天才ベスト10に余裕で入る天才中の天才の数学者である。ノイマン宇宙人説があるくらいの天才である。
だからこのゲーム理論ももちろん「とんでも学問」の部類ではない。
ゲーム理論の中に「囚人のジレンマ」というモデルがある。これはとてもイメージしやすいモデルなので、ゲーム理論=囚人のジレンマ的に説明されることもよくある。
「囚人のジレンマ」の説明に入る前に、その中で重要な役割を果たす「ナッシュ均衡」について説明する。というか「ナッシュ均衡」の説明は、ほぼほぼ「囚人のジレンマ」の説明であるといえる。
「ナッシュ均衡」は数学者のジョン・ナッシュによって発見された概念である。ナッシュもまた天才数学者であるが、一時期統合失調症を患い、波瀾万丈な人生を送った。彼の半生は映画「ビューティフル・マインド」に描かれている。この映画には「ナッシュ均衡」の話はほんの少ししか出てこないが、映画としてとても面白いのでお勧めである。
で、「ナッシュ均衡」の話。
「ナッシュ均衡」の正しい説明もまたやっかいだ。ググるとこんな説明がされている。
「どのプレイヤーも、他のプレイヤーがそのナッシュ均衡の戦略を選んでいるもとでは、その戦略が一番利得が高くなる」
※ゲーム理論では、私やら他の人を「プレイヤー」と呼ぶ。
なんか、よくわからない。。。
そこで自分はよくこういう説明をする。これが正確に「ナッシュ均衡」の説明になっているかは少し自信がないが、どういう仕組みかは体感しやすいと思う。
ここにケーキが1つある。これを2人で分けるとする。

どちらも食いしん坊で、内心、隙あらば大きいカットを食べたいと思っている。また、二人の関係性に寄るところが大きいと思うが、仮に全ての状況が対等だとする。
さて、実際にどういう配分でケーキはカットされるだろう。
一人が分けてその人が選ぶとしたら結果は自明だ。その後、惨事が起こることは間違いない。
だれだって、自分の取り分を大きくしたい。「人間だもの」
そこでこういうルールにする。
プレイヤーAがケーキを分けるなら、プレイヤーBがカットを選ぶ。


なるべく自分が大きなカットを手に入れたいと思うが、カットの大きさを不均等にすれば、大きなカットは相手が持っていってしまうに違いない。そこでもっともリスクが小さい戦略は、きっちり2等分することとなる。
このようにお互いの利得(ゲーム理論では、損得のことを「利得」という言い方をする)が関係し合っている場合、自然とあるバランス(均衡)に落ち着く。
だいたい、そんなイメージである。

ここで大事なのは、「プレイヤーAがケーキを分けるなら、プレイヤーBがカットを選ぶ」というルールの設定だということを少しだけ記憶の端に置いておいてもらっていただければ幸い。(まとめの話に絡むので)
さて、「囚人のジレンマ」の話。
こんなシチュエーションを考えてみる。
ネコAとネコBはいつも一緒に盗みを働く泥棒二人組。
日ごろから二人は「もし捕まっても絶対に口を割らないようにしような!」と強く誓い合っていた。

しかし、ある日、悪運がつきて二人同時に捕まってしまう。

二人は別々の取調室で取り調べを受けることになった。
二人とも当然「黙秘」(協調)するつもり満々である。

その時、刑事は、取引をもちかけた。
「本来なら、お前たちは懲役5年である。」
「ただ、二人とも黙秘したら、証拠不十分で二人とも懲役2年になる。」
「もし、一方が黙秘して、一方が自白したならば、自白した方は無罪放免にしてやる。
しかし、逆に、黙秘した方は懲役10年に増える。」
「二人とも自白したら、本来通り、二人とも懲役5年になる。」
「さあ、お前はどうする?」
図に表すとこんな感じだ。
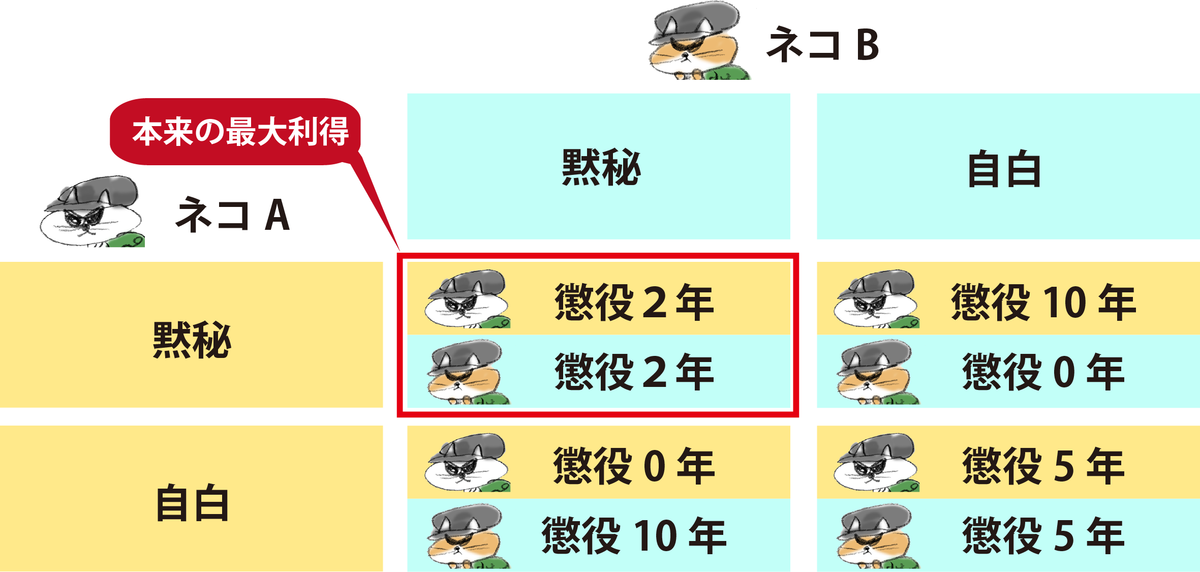
一見して、「二人とも黙秘する」(懲役2年)がもっともよい選択だ。では、その「戦略」が選ばれるかというと、実はそうはならない。
ネコAの立場になって考えてみる。
(もし、ネコBが捕まる前の約束通り「黙秘」しているとしよう。その場合、おれも「黙秘」すれば、懲役2年。しかし、裏切って自分だけ「自白」したら、おれは無罪放免だ。だとすれば、「自白」したほうが得だ)
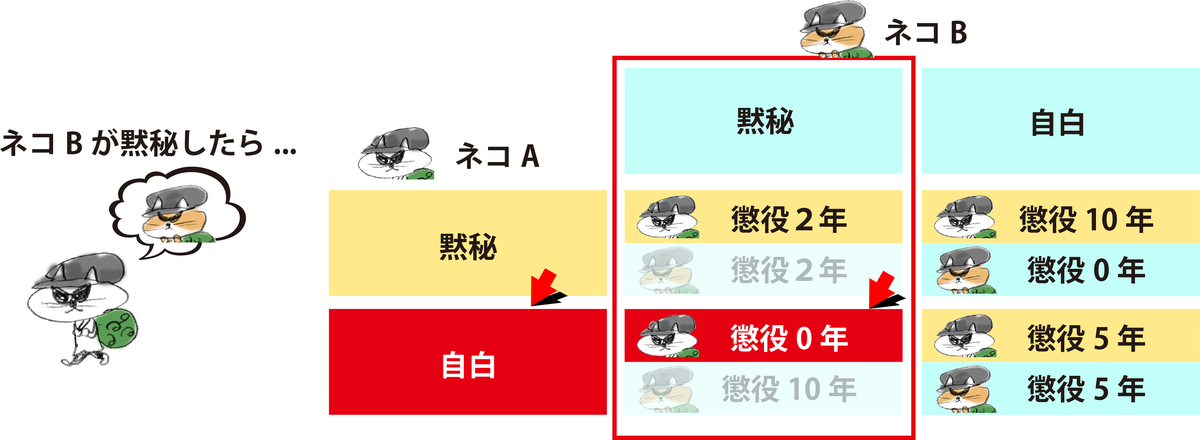
(逆に、ネコBが裏切って「自白」したらどうだろう。おれが「黙秘」したら、おれだけ懲役10年になっちまう。おれも「自白」すれば、元々の5年の刑。10年は避けたい。だとすれば「自白」したほうがマシだ)
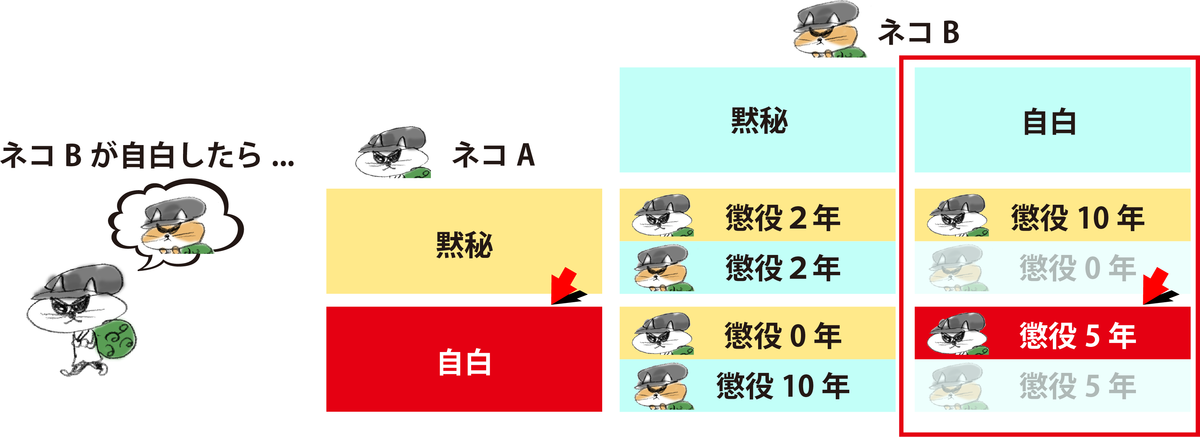
こうして、ネコBがどっちに決断しようが、ネコAは「自白」を選ぶことになる。
ネコBの立場に考えても同じ事が言える。
結局ネコAもネコBも、相手の判断に関係なく「自白」つまり「裏切り」を選ぶことになる。
このように、本来なら互いに協調(黙秘)したほうが互いに得になるのはわかっているのに、自分の利得を考えるとどうしても裏切り(自白)を選んでしまう。
お互いのことを信じ切れないため、わかってても最善の手を打てない。そういうジレンマを抱えることから「囚人のジレンマ」の名がついている。
ちなみに、こうしたバランスに自然に落ち着いていくことを「ナッシュ均衡」という。
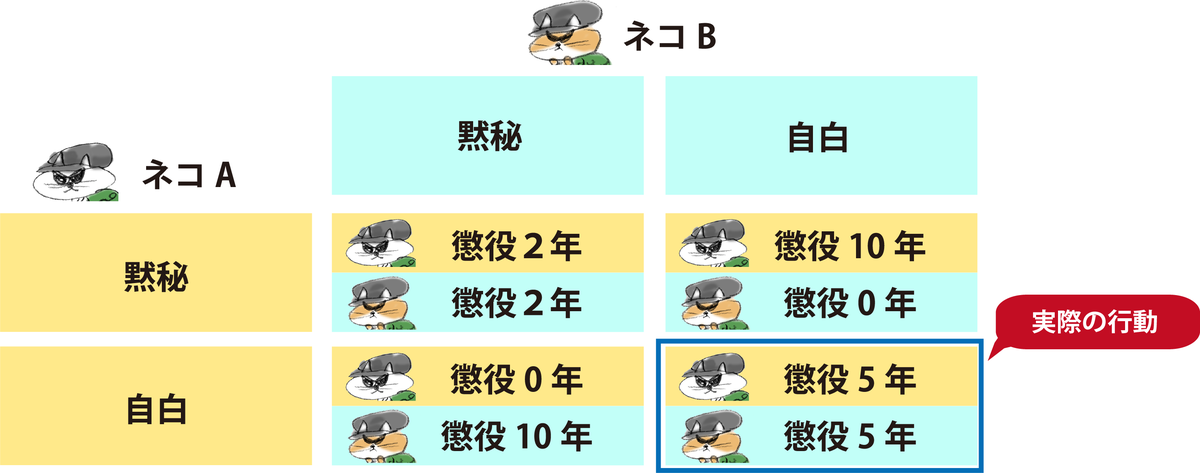
これを読んでくれてる人は、ほとんど泥棒稼業の人じゃないだろうから、自分には関係ない話と思うかもしれないが、こうした「ジレンマ」は実際の生活でも起こる。
近々で言えば「トイレットペーパーありません」事件だ。
元は「トイレットペーパーの原材料は中国で生産されているので、武漢が閉鎖されてトイレットペーパー不足が起こるぞ!というデマから始まった騒動だ。
オイルショックを経験している身としては、「はいはい、またですか。懲りないねー」的なお話だが、結局、一定の期間、実際にトイレットペーパーが店から消えてしまった。
この事件も「囚人のジレンマ」のモデルにあてはめることができる。
この場合は、「黙秘」(協調)が「買いだめに走らない」、「自白」(裏切り)が「買いだめする」に相当する。刑期はちまたの噂やその人の予想による値となる。科学的な根拠がない値でも、その人やある集団がそう思った値でも成立してしまうのが、ミソというか困ったところだ。
図にするとこんな感じになる。
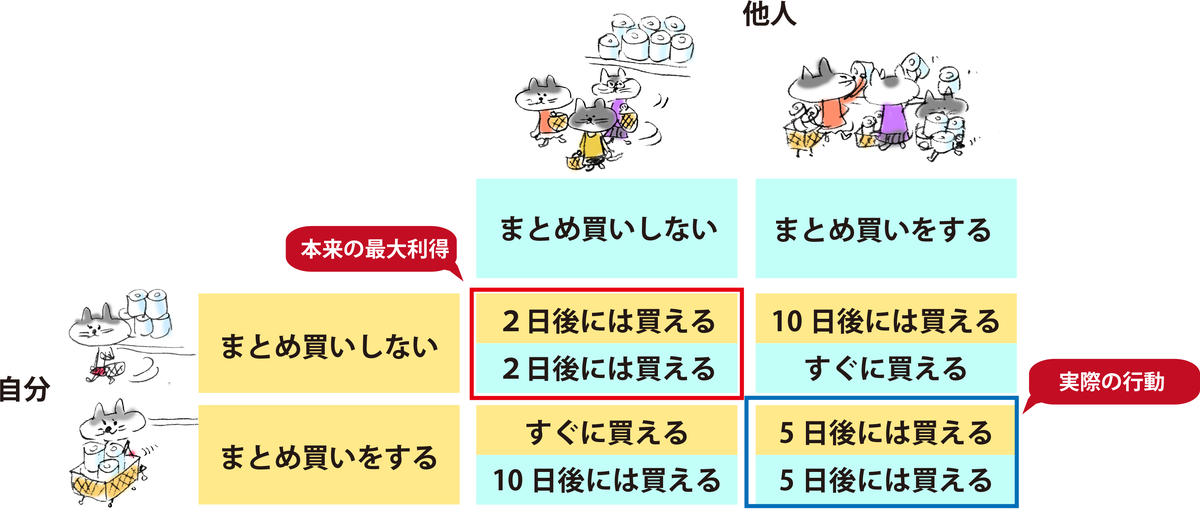
「囚人のジレンマ」と同じ流れで、本来なら互いに協調(買いだめしない)したほうが互いに得になるのはわかっているのに、自分の利得を考えるとどうしても裏切り(買いだめ)を選んでしまう。
お互いのことを信じ切れないため、わかってても最善の手を打てず、トイレットペーパー不足を起こしてしまう。そして実際に起こった。
もっとも今回は、元ネタが根拠がないことがすぐに伝わったためか、オイルショックの時より早く収まった気がする。(よかった)
まとめ。
集団の心理が複雑に絡まって起こる出来事は、原因解明も未来の予測も複雑で不透明なものになりそうだが、実は意外とシンプルなモデルで説明がつくというのが面白い。
必ずしも、我々はわかっていても「みんなのための最善手」を選べないというのもおもしろい。「みんなが理性的に動けば世の中うまくいくはずだ」的な理想論を唱えるより、人ってのはそういう矛盾と葛藤を抱えて生きてるのだ。「人間だもの」。そういう心づもりでいた方がよっぽど現実的に対処できそうだ。
最後に、ケーキの分け方でいえば、一方が切り、一方が選ぶというルールがあってこそ、2等分される。これが切る者、選ぶ者、ともにジャンケンで選ぶなんてすると2等分することにならない。また、トイレットペーパー問題では、数値は科学的な根拠がないので、まとめ買い(裏切り)でも、「(在庫は十分にあるはずなので)2日後には買える」と自分で補正できれば、「共に裏切る」という均衡には陥らなくて済む。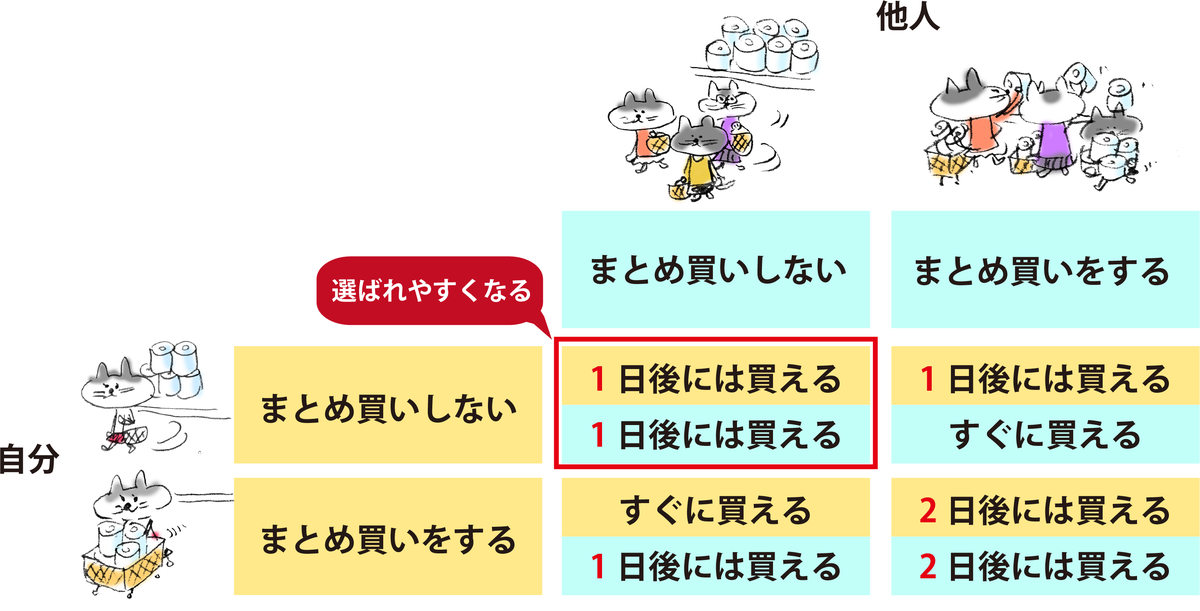
実際に、[自粛する/自粛しない]問題では、「みんな自粛しない」(共に裏切る)に陥ることになりそうだけど、実際のところはそうなっていない。
それは、たとえば、
自粛するは(協調する)は、精神衛生上は×であるが、自粛時間が短くなる。また、自粛要請に応じたら協力金がもらえる。逆に自粛しない(裏切り)の利得は、精神衛生上は◎であるが、罰則というペナルティーがあるというように利得がルール(例えば法律)によって補正されているため、必ずしも「みんな自粛しない」(共に裏切る)でナッシュ均衡にならないようになっているためだ。
複雑になるというか、を追加することで、利得バランスが調整できることを意味する。つまり、
ゲーム理論に従って、どんなにあがいても「人間だもの」的なところに陥ってしまうと落胆する必要はなく、ルール(例えば法律)を調整したり、各自の知見を高めてより正しい数値を見いだせれば、よりよい結果(共に協調)を得られうるということだ(むしろ、こっちがゲーム理論の本命題のような気がする)。
=============================================
神様のゲーム#1 https://tech.morikatron.ai/entry/2020/03/25/100000
神様のゲーム#2 https://tech.morikatron.ai/entry/2020/04/01/100000
神様のゲーム#3 https://tech.morikatron.ai/entry/2020/04/10/100000
神様のゲーム#4 https://tech.morikatron.ai/entry/2020/04/17/100000
神様のゲーム#5 https://tech.morikatron.ai/entry/2020/05/18/100000
神様のゲーム#6 https://tech.morikatron.ai/entry/2020/05/28/100000
神様のゲーム#7 https://tech.morikatron.ai/entry/2020/06/04/100000
神様のゲーム#8 https://tech.morikatron.ai/entry/2020/07/06/100000
=============================================